스도쿠(sudoku) 푸는 법: '드러난 셋(naked triple)'의 의미 및 추론 방법

이 글에서는 스도쿠 공식 중 '드러난 하나'와 '드러난 둘'의 의미와 추론 방법을 다룹니다. '드러난 셋'은 세 개의 숫자 또는 그 부분집합의 조합으로 이루어진 세 개의 칸을 의미하며, 다른 칸에서 이 세 숫자를 지움으로 후보숫자의 수를 줄일 수 있습니다.

목차
1. 서론
2. 드러난 셋의 의미
3. 드러난 셋의 추론 방법

 

1. 서론

이전 포스팅에서는 스도쿠의 규칙 및 후보 숫자를 채워 넣는 방법, 그리고 가장 기본적인 공식인 '드러난 하나'와 '드러난 둘'에 대해 다루었습니다. 앞의 포스팅을 안 보신 분들은 아래의 세 포스팅을 먼저 읽어보시길 추천드립니다.

 

 

첫 번째 포스팅: 스도쿠 규칙 및 가장 기초적인 풀이방법 보러가기 ↓

스도쿠(sudoku) 푸는 법: 스도쿠 규칙 및 가장 기초적인 풀이법

 

두 번째 포스팅: 스도쿠 공식을 적용하기 위한 전제조건 보러가기 ↓

스도쿠(sudoku) 푸는 법: 스도쿠 공식을 적용하기 이전에 해야 할 일

 

세 번째 포스팅: '드러난 하나(naked single)'와 드러난 둘(naked pair)'의 의미 및 추론 방법 보러가기 ↓

스도쿠(sudoku) 푸는 법: '드러난 하나(naked single)'와 '드러난 둘(naked pair)'의 의미 및 추론 방법

 

 

이 포스팅에서는 지난 포스팅에 이어 스도쿠 공식을 설명하는 용어 중 ‘드러난(naked)’ 것과 ‘숨겨진(hidden)’ 것의 의미를 계속 다루어 보겠습니다. 지난 포스팅에서 이미 '드러난 하나'와 '드러난 둘'을 다루었으며, 오늘의 포스팅에서는 아래의 표에서 노란색으로 칠한 '드러난 셋'에 대해 설명해 보겠습니다.

 

스도쿠 공식 싱글, 페어, 트리플의 종류

 

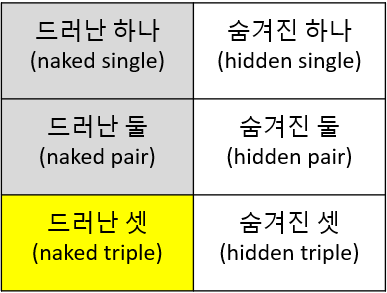
2. 드러난 셋의 의미

지난 포스팅에서 후보숫자가 하나 밖에 남지 않은 칸을 '드러난 하나'라고 한다는 것, 그리고 한 쌍의 숫자가 동일하게 두 칸에 들어있는 경우를 '드러난 둘'이라고 한다는 것을 다루었습니다. '드러난 하나'의 경우에는 후보숫자가 곧 답이 되며, '드러난 둘'의 경우 해당하는 두 숫자를 다른 칸의 후보숫자에서 지울 수 있습니다. '드러난 셋'은 '드러난 둘'과 매우 유사하기 때문에 '드러난 둘'의 원리를 이해하면 비교적 쉽게 이해할 수 있기 때문에 '드러난 둘'의 원리가 이해 안 가신다면 앞의 포스팅을 참고해 보시기 바랍니다.

 

드러난 셋의 정의

아래의 그림에서 볼 수 있듯이, '드러난 셋'은 세 개의 숫자 또는 그 부분집합이 세 개의 칸에 들어 있는 것을 말합니다. 아래의 예에서 노란색, 파란색, 연두색으로 칠한 세 개의 칸이 드러난 셋을 이루는데, 연두색으로 칠한 칸에는 (5, 6, 9)의 세 숫자가 모두 들어 있는 반면 노란색 칸과 파란색 칸에는 (5, 6, 9)의 부분집합인 (5, 9)와 (6, 9)가 각각 들어있습니다. 다시 말해, 세 숫자를 모두 포함하지 않고 그 일부만을 포함할 경우에도 '드러난 셋'을 이룰 수 있습니다.

 

스도쿠 공식 '드러난 셋'의 예시

 

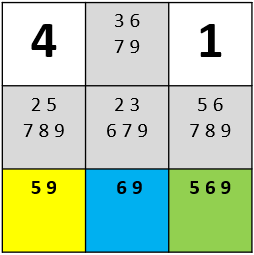
드러난 둘과 드러난 셋의 차이점과 공통점

'드러난 셋'을 좀 더 알기 쉽게 설명하기 위해 '드러난 둘'과 비교해 보도록 하겠습니다. 앞선 포스팅에서 설명한 것과 같이 '드러난 둘'에서는 두 개의 칸에 두 숫자가 동일하게 포함된 경우에만 적용됩니다. 하지만 '드러난 셋'의 경우에는 세 숫자의 조합에 대한 부분집합도 포함됩니다. 

 

'드러난 둘'과 '드러난 셋'의 공통점은 '드러난 둘'에 해당되는 두 칸과 '드러난 셋'에 해당되는 세 칸이 하나의 닫힌 계를 이룬다는 것입니다. '드러난 둘'에 해당되는 두 칸에는 해당되는 두 개의 숫자 이외에 다른 숫자가 들어갈 수 없습니다. '드러난 셋'에 해당되는 세 칸에도 해당되는 세 개의 숫자 이외에 다른 숫자가 들어갈 수 없습니다. 

 

 

3. 드러난 셋의 추론 방법

결론부터 말씀드리면 세 개의 칸에 들어있는 세 숫자가 '드러난 셋'을 이루는 경우 다른 칸에서는 후보 숫자 중에 이 세 숫자를 지워줄 수 있습니다. 즉, 위의 그림에서 회색 칸들에는 숫자 5, 6, 9가 들어갈 수 없다는 것을 확실히 알기 때문에 지워줘도 된다는 것입니다. 이미 이해하신 분도 계시겠지만 왜 그런지 한 번 설명해 보겠습니다.

 

만약 노란색 칸에 숫자 5가 들어간다면 파란색 칸에는 6 또는 9가 들어가야 합니다. 만약 파란색 칸에 6이 들어간다면 연두색 칸에는 9가 들어가게 됩니다. 파란색 칸에 9가 들어간다면 연두색 칸에는 6이 들어가게 됩니다.

만약 노란색 칸에 숫자 9가 들어간다면 파란색 칸에는 6이 들어가게 되며, 연두색 칸에는 5가 들어가게 됩니다. 

 

그러므로 노란색, 파란색, 연두색 칸에 들어갈 수 있는 숫자의 조합은 (5, 6, 9), (5, 9, 6), (9, 6, 5) 밖에 없다는 것을 알게 됩니다. '드러난 셋'에 해당되는 다양한 경우에 따라 가능한 조합의 수는 달라질 수 있습니다. 그러나 중요한 점은 어떤 경우에라도, 세 숫자는 해당 세 칸 안에서 해결을 보게 됩니다. 따라서 이 세 칸을 제외한 다른 칸에는 5, 6, 9가 들어갈 수 없게 됩니다. 따라서 회색 칸들에서 5, 6, 9를 지워주면 다음과 같은 결과를 얻을 수 있습니다.

 

스도쿠 공식 '드러난 셋' 추론 방법

 

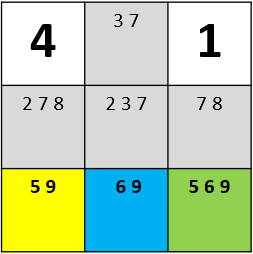
세 숫자를 지워준 결과, '드러난 하나'나 '드러난 둘' 등 남은 칸의 정답을 알 수 있는 단서는 나타나지 않았습니다. 하지만, 회색 칸들에 들어갈 수 있는 후보숫자의 수는 현저하게 줄어든 것을 알 수 있습니다.

 

앞선 포스팅에서 언급한 것처럼 이러한 공식은 열, 행, 상자를 포함하는 모든 유닛에 적용할 수 있습니다. 이렇게 각각의 유닛에 대해 후보숫자를 줄여나가다 보면 정답이 확정되는 칸이 나타나게 되며, 확정된 정답을 통해 또다시 다른 칸의 후보숫자를 줄여나갈 수 있게 됩니다.

 

이와 같이 지난 번 포스팅에 이어 '드러난 하나', '드러난 둘', '드러난 셋' 공식을 모두 살펴보았습니다. 같은 원리로 '드러난 넷'도 가능합니다. '드러난 넷'은 네 개의 칸에 네 숫자의 조합이 들어가면 됩니다. '드러난 넷'은 직관적으로 찾기 어렵기 때문에 앞의 셋에 비해 비교적 활용성이 떨어지는 편이지만 나중에 기회가 되면 한 번 따로 다루어 보도록 하겠습니다. 다음번 포스팅에서는 '숨겨진 하나(hidden single)'와 '숨겨진 둘(hidden pair)'에 대해 설명해 보도록 하겠습니다.